This post is a summary of a paper written with Mathieu Huard and Micheal Eigensatz from Evolute presented at AAG 2014 at UCL in london. Both of them were at the origin of the optimization idea and invited me to play with their new toy. The post will present mostly the second part of the article which I was mostly involved with , using some extract from the article itself.
“Repetition is a key factor in reducing complexity and cost in the design, engineering, construction, fabrication, and logistics of an architectural project. Trying to achieve a high repetition of elements in a freeform structure, however, is a challenging endeavour. A major restriction comes from the requirement of smoothness”. “Due to the increasing popularity of NURBS modelling tools,, research in architectural geometry has put a strong focus on the approximation of smooth freeform surfaces.” […] “In practice, however architects, builders, and designers have always been intrigued by non-smooth structures as well. Also in nature, we find appealing and inspiring non-smooth architectures”,interestingly often involving repetition”. And in fact, dropping smoothness turn out to be” a key ingredient of our approach to design freeform structures with extreme repetition”
“Working with repeating elements for practical or aesthetical reasons has a long tradition in architecture. Figure 1 lists a small subset of related work. The principle of surface discretization can be found from the earliest constructions such as the great pyramid of the Giza or the Mayan Pyramid. More than being only a technological answer to the act of fabricating and erecting huge constructions from smaller repetitive elements, these discretizations are a design potential to create new tectonics to serve the building aesthetics. In the end of the 15th century, Ferrara Biagio Rosseti utilized facetted stones to define the appearance for the Palazzo dei Diamanti. More recently, crystalline or diamond like structures have been used as poetic reference. The Harpa concert hall of the Henning Larsen architects in Reyjavick and the Oxford Street in London facade by Future Systems architects are good examples of both facetization and heavy repetition. In the early 50ies, the research by Konrad Wachsman and Buckminster Fuller on large span structure led to what is now called space frames. These structures were conceived as fully prefabricated systems with a few number of component types .These may vary in dimensions but stay repetitive as a component. They also take advantage of the structural potential of highly triangulated geometry. A more recent project, the Beijing Water Cube by PTW architects is based on a Wearie-Phelan voxelization of space, which is related to our Voxel Meshes, though no repetition was used to our knowledge. A third family of projects should be mentioned, starting with the seminal project built in Montreal, Habitat 67 by Moshe Shafdie for the world expo. Constituted of prefabricated blocks of the size of a room, which are interlocked between one another, the habitation building is a gigantic Lego game. Similar projects were built by representants of the Japanese avant-garde, the Metabolist group, which designed megastructure based on prefabricated elements in the early 70ies, i.e., the Capsule hotel in Tokyo of Kisho Kurokawa. Finally, a French architect, Jean Renaudie with his habitation project in the center of the new town of Ivry built from 1971 to 1980, has a similar approach than Habitat 67, spreading the building horizontally and vertically in order to maximize the sun exposure and providing inhabitants with large terraces and private gardens.”
May be last but not least, a reference which found after writing the article, pointed out by Jacques Raynaud (RFR) , the great work of Zvi Hecker, which deserve a bit more attention for its radical nature and its harsh poetic.(Fig2 and 3)
“While based on different geometric techniques, all of these works are based on related principles such as repetivity, prefabrication, and non-smoothness. and constitute a great source of inspiration “
In the first part of the article, Mathieu presents his work on optimization of freeform surface with equilateral triangles, pushing the idea of using the reference surface more “as control shapes to guide the results towards the desired features”, “The idea is to loosely approximate general surfaces, far beyond usual tolerances.” (see article for more detail) In the last part, the concept is pushed further into another direction: the Voxel Meshes which is the subject of this post.
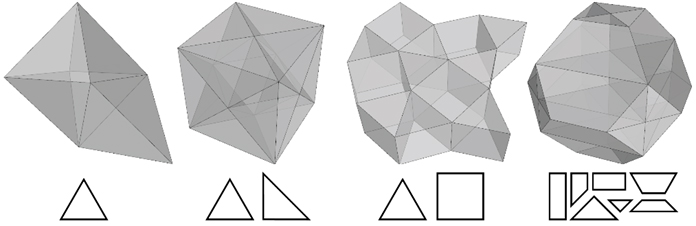
We start with some regular polyhedra (voxels) that can be repeated to fill the entire three dimensional space. Since we only use a few different voxels, only a few different polygonal shapes will fill (or better scatter) the entire space in a very structured way. We can then cut through this space and ”carve out” a connected (2-manifold) sheet of polygons that defines a panelization with a repetition of only those initial few polygonal shapes used to fill the space.
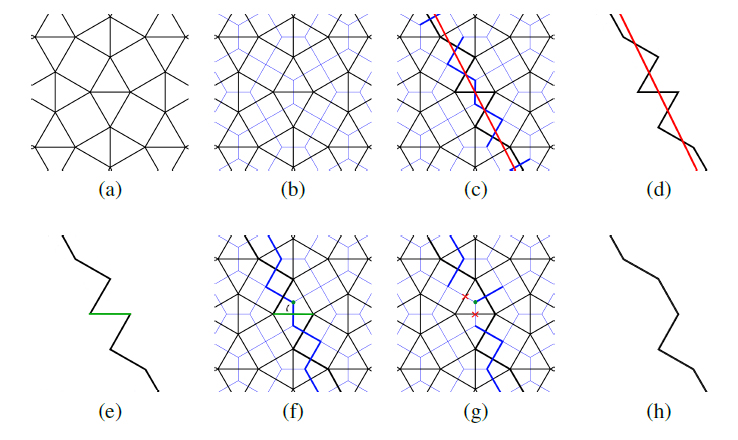
Fig5:2D illustration of the basic principles of Voxel Mesh generation. (a)-(d) Show the generation of a Voxel Mesh sheet: (a) Voxelization of the entire space using a block of two voxels (a triangle and a square) as the generator. Thus the space is filled by line segments of equal length. (b) The dual graph (blue) of the voxelization. (c) The dual graph is cut with a reference surface (a curve in 2D, here a simple line in red). The edges of the dual graph that are cut by the line are highlighted in thicker blue. Each of those edges has a corresponding voxel line segment, highlighted in thicker black. The collection of all those highlighted line segments build the final Voxel Mesh sheet (a polyline in 2D) out of highly repetitive elements, shown in (d), following the design surface. The bottom row (e)-(h) shows a local update operation: (e) The user selects one of the elements (line segments in 2D) to update, highlighted in green. The Voxel Mesh sheet can now be locally updated in one of the two possible directions defined by the corresponding dual graph edge. The dual vertex indicating the update direction is shown as a green point in (f). All dual edges incident to this vertex flip their state: active edges become inactive and vice versa, shown in (g). The new set of active edges (highlighted in thick blue) define the updated Voxel Mesh sheet (h).
1) Voxelization of the 3D space. 2) Extracting a manifold sheet (the Voxel Mesh) by cutting a dual graph. 3) Providing means to manually update and refine the Voxel Mesh.
The output presented below show some pattern which I found somewhat fascinating .They are reminders of the work of the 60ies on the Cote d’azur, such as La Grande Motte from Jean Balladur.
Same idea of repetition , same feeling of boredom but at the same time of constantly variating pattern. Depending of the reference surface, of its orientation in the Voxel box, some very different pattern can be achieved with the same level of the repetition. The same relentless mathematical rigor with some unexpected twist, which makes these patterns alive as the sun travel through the day.
With fully free form surface, one can easily , reshape full landscape mixing elements of structure and vegetation
We also noticed that depending of the generator of the voxel mesh , some facet have some preferential orientation. Depending of these orientation , we can decide of there materiality or fonctionality. For instance, some facets oriented toward the sky could be used for sun harvesting system, solar cell, or growing plants, but also just let light in.
In the following simulation we used this orientation to block view or let light in. Giving in some case , an apparently opaque facade which is with an other orientation or point of view , a almost fully transparent one.
“The Voxel Meshes offer a large potential for future work: Since they define a highly structured design space, they could well serve as the basis to optimize for environmental or functional objectives via combinatorial optimization. This potential is already shown in some of the results: the strong underlying structure makes it easy to for example select all panels facing a given direction, and making themtransparent or opaque, optimizing for lighting conditions. Approaching this in a more systematic and automated manner offers a strong potential for lighting and shading optimization. Additionally, instead of just using a single sheet, two or more sheets could be extracted to form a volumetric space frame structure with identical members.”